The Moon is getting further away from Earth. Where does this extra energy come from?

All bounded orbits where the gravity of a central body dominates are elliptical in nature. In the case of the Moon orbiting the Earth, the eccentricity of the ellipse is so small (0.055) that it is almost a circle:

Therefore, the gravitational force F_g that the Earth exerts on the Moon is perpendicular to Moon's velocity v, so it is a centripetal force F_c, making the trajectory of the Moon bend:
$$F_{g}=F_{c} \\ \frac{GMm}{r^2}=\frac{mv^2}{r}$$ where G is Newton's constant, M is Earth's mass, m is Moon's mass and r is the radius of the orbit.

This implies that the kinetic energy of the Moon is
$$K=\frac{1}{2}mv^2=\frac{GMm}{2r}$$ which is smaller than the absolute value of the potential energy
$$U=-\frac{GMm}{r}$$ So the mechanical energy of the Moon is
$$E=-\frac{GMm}{2r}$$

We know that at the time of its formation, the Moon sat much closer to the Earth, a mere 22,500 km away, compared with the 402,336 km between the Earth and the Moon today. So the Moon is getting further away from Earth, now at the rate of 3.78 cm per year. Nevertheless, according to the last equation, a larger r means that the Moon has more energy every year. Is its energy non conserved? Who is giving energy to the Moon?

Can an object exceed the speed of light if we push it for enough time?

The second Newton's law of motion establishes that, in an inertial reference frame, the vector sum of the forces F on an object is equal to the mass m of that object multiplied by the acceleration vector a of the object. That means that if we apply a constant force on a body without friction, then the object will move with constant acceleration, increasing its speed by the same amount every second.

The acceleration is proportional to the force, so if the net force is 100 Newtons and the mass is 2 kilograms, the acceleration will be 50 meters per second every second. But if the force is 2 N, the body will increase its speed by 1 m/s every second. Notice that this is not a huge acceleration. Nevertheless, if we keep pushing and wait for 300000000 seconds (9.5 years) the object will move faster that light.

But we know that nothing can exceed the speed of light. This is a well-established law of nature whose confirmation has become routine in current particle accelerators.

Try to find the solution to this contradiction!

Please, explain your reasoning. You can post your attempted answers in the comment box below. Please, do not use Facebook or Twitter to give your answers.

Is hydrogen atom in bifluoride connected by two covalent bonds?

In chemistry, a valence electron is an electron that is associated with an atom, and that can participate in the formation of a chemical bond. In a single covalent bond, both atoms in the bond contribute one valence electron in order to form a shared pair. For instance, hydrogen atoms have one valence electron, while oxygen atoms have two. That is why a water molecule contains one oxygen and two hydrogen atoms that are connected by singles covalent bonds:

By Dbc334 (first version); Jynto (second version) - File:Water-3D-vdW.png, Public Domain, https://commons.wikimedia.org/w/index.php?curid=1332739

So the Lewis structure of water is H-O-H.

But let us consider a more complex example: bifluoride. Bifluoride is an inorganic anion with the chemical formula [HF₂]⁻.

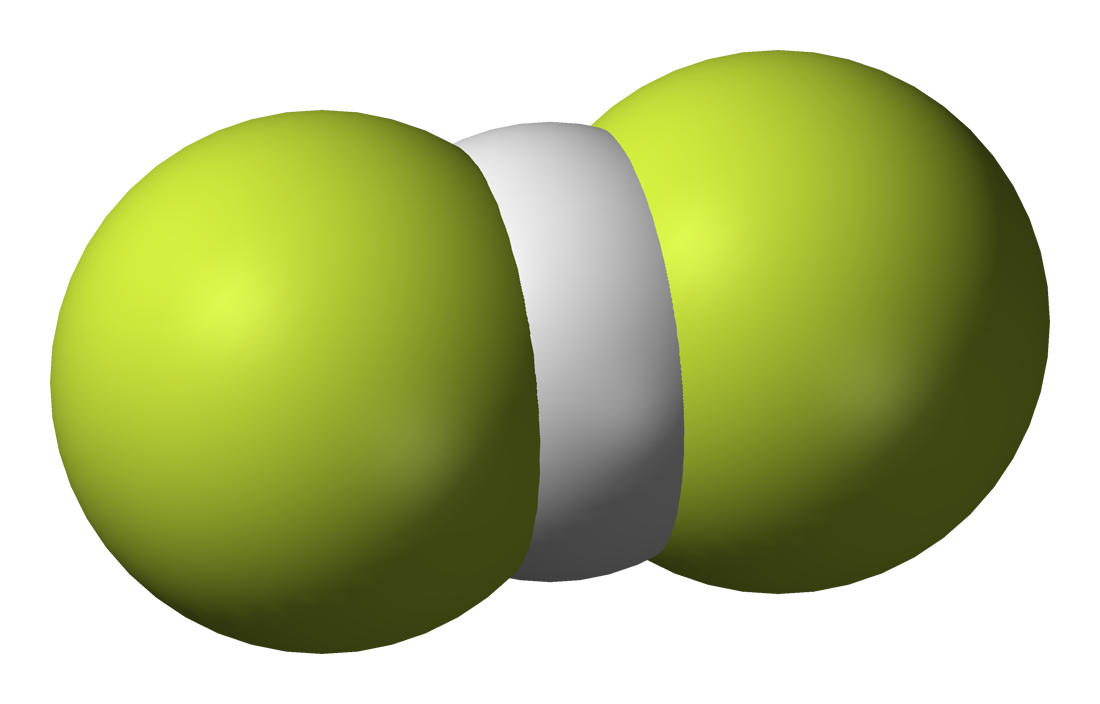Public Domain, https://commons.wikimedia.org/w/index.php?curid=1496287

It is not a strange anion. Some [HF₂]^- salts are common, examples include potassium bifluoride (KHF2) and ammonium bifluoride ([NH4][HF2]).

As shown in the figure above, the structure of the anion is symmetric, with the hydrogen situated in the mid-point of the F-F distance. In addition, the H-F contacts in this ion are very short, like in covalent bonds, and the corresponding H.F interactions are also strong enough to be classified as covalent bonds. So the corresponding Lewis structure of the anion should be [F-H-F]^-. But, how is this possible? Hydrogen atoms have one valence electron. They cannot be connected by two covalent bond!

Are you able to give an explanation? Accept the challenge!

Please, explain your reasoning. You can post your attempted answers in the comment box below. Please, do not use Facebook or Twitter to give your answers.

Is expansion of gases a violation of inertia law?

The first Newton's law (also called inertia law) says that, when viewed in an inertial reference frame, an object either remains at rest or continues to move at a constant velocity, unless acted upon by a net force.

Let us suppose that we have a box with a wall splitting it in two halves. The left half contains a rest gas (no wind inside), while the right half is empty. Suddenly, we remove the wall. Because of the fact that gases expand to fill their containers, we know that the gas of the left half will move to the right side in order to fill the whole box:

But there is no net force acting on the gas, so why has it moved to the right half of the box? Do gases violate the inertia law?

Are you able to give an explanation? Accept the challenge!

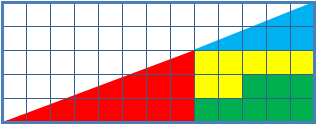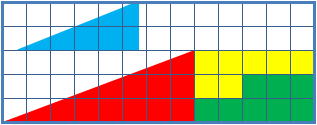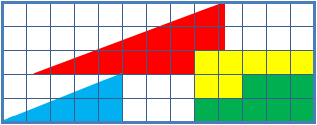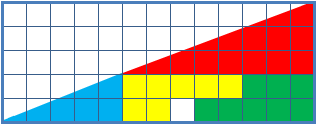
Can we obtain extra surface by assembling the pieces in a different way?

Picture A and B show different arrangements made of similar shapes in slightly different configurations:

By Krauss (Own work) [CC BY-SA 4.0 (http://creativecommons.org/licenses/by-sa/4.0)], via Wikimedia Commons

So the question is: where does the extra one unit square come from?

By Trekky0623 at English Wikipedia (Transferred from en.wikipedia to Commons.) [Public domain], via Wikimedia Commons

Are you able to solve this puzzle?

If nuclear fusion is the reverse of fission, why is energy released in both processes?

Nuclear power is the use of nuclear reactions that release nuclear energy to generate heat. There are basically two ways to release energy from nuclei:

• nuclear fission, which is either a nuclear reaction or a radioactive decay process in which the nucleus of an atom splits into smaller parts (lighter nuclei).  This released energy is the one that is frequently used in steam turbines to produce electricity in nuclear power plants.

Public Domain, https://commons.wikimedia.org/w/index.php?curid=486924

• nuclear fusion, which is a reaction in which two atomic nuclei fuse to form a heavier nucleus. Nuclear fusion reactors are not yet economically viable, but this technology is currently under research and it could become viable in a few decades.

By Wykis - Own work, based on w:File:D-t-fusion.png, Public Domain, https://commons.wikimedia.org/w/index.php?curid=2069575

If splitting a nucleus into two smaller nuclei releases energy, it seems that combining two smaller nuclei into one larger nucleus would require energy, not release it, because it is the inverse process. So, why can we obtain energy from both processes?

 Are you able to resolve this cognitive conflict?

Please, explain your reasoning. You can post your attempted answers in the comment box below. Please, do not use Facebook or Twitter to give your answers.

Why are cognitive dissonances useful for teaching?

Psychologists define cognitive dissonance as the mental stress or discomfort experienced by an individual who holds two or more contradictory beliefs, ideas, or values at the same time, performs an action that is contradictory to one or more beliefs, ideas, or values, or is confronted by new information that conflicts with existing beliefs, ideas, or values. It has been found that an individual who experiences a cognitive dissonance tends to become psychologically uncomfortable, and is motivated to try to reduce this inconsistency [Festinger, L. (1957). A Theory of Cognitive Dissonance. California: Stanford University Press].

That is why psychologists have incorporated cognitive dissonance into models of basic processes of learning, notably constructivist models [Ausubel, David P.,Novak, J.D.,Hanesian, H. (1978) Educational Psychology: A Cognitive View (2ª ed.). New York: Holt, Rinehart and Winston.] [Ausubel, David.P. (2000). The Acquisition and Retention of Knowledge. Dortrecht, Netherlands: Kluwer.].

In these models teachers gather information about students’ existing ideas and use this information to design activities that foster dissonances in their minds by increasing their awareness of conflicts between students’ prior beliefs and new information (e.g., by requiring students to defend prior beliefs and confronting them with unexpected experimental results or different ideas). Then, teacher guides students to find by themselves correct explanations that resolve the conflict.

Notice that with this methodology no external reward is needed. Cognitive dissonances are enough to increase students' enthusiasm for educational activities. Some researchers have concluded that students who are forced to attribute their work to this intrinsic motivation came to find the task genuinely enjoyable [Aronson, E. (1995). The Social Animal. New York: W.H. Freeman and Co.].

Once students have found by themselves the correct explanation that resolve the cognitive dissonance, a conceptual change has happened. Now, students do not see the world with the same eyes as before, and this change will remain forever, so they keep easily what they have learned even several years before. In fact, it has been shown that teaching methodologies based on cognitive dissonances significantly increase learning in science and reading [Guzzetti, B.J.; Snyder, T.E.; Glass, G.V.; Gamas, W.S. (1993). "Promoting conceptual change in science: A comparative meta-analysis of instructional interventions from reading education and science education". Reading Research Quarterly 28: 116–159.].

Therefore, we can say that we have found a magic wand that will make the students learn science! Nevertheless, things are not so easy. The really difficult part of this process is to find the suitable cognitive dissonances that make the students learn every specific chunk of scientific knowledge. And this is a too technical task to be left to psychologists! Scientists should do it. That is why I have created this web site, to make a database of questions/interventions that could help teachers to foster dissonances in student minds. Of course, since we are looking for cognitive conflicts with students beliefs, the way we can foster these conflicts depends strongly on the students. So,

• If you are a teacher, you have to select the most suitable question/intervention in each case. You can also collaborate with this project by sharing the questions/interventions that you use to foster dissonances in your students.
• If you are a student, enjoy trying to resolve the conflicts. You can post your trials in the comment box below each puzzling question. Some weeks after each publication we will include the explanations that eliminate the inconsistency.  

I hope you found this web site useful!

Sergio Montañez
Founder of Cognitive Dissonances